Towers of Hanoi
Contribution of this section
use of lists,
use of functions,
use of data µ-calculus formulae.
New tools: mcrl2xi.
The Towers of Hanoi is a classic mathematical puzzle that involves three pegs
(numbered 1, 2 and 3) and `N >= 1 discs. Every disc has a unique
diameter and has a hole in the center so that it can slide onto any of the pegs.
The discs are numbered 1 to N increasingly with their sizes. Initially,
all discs are stacked onto peg 1 in increasing size from top to bottom (see the
figure below where N = 6). The puzzle is solved when all discs are on
peg 3 in the same order. Discs can be moved from one peg to any other, as long
as the following rules are obeyed:
Only one disc can be moved at a time.
Only the topmost disc on a peg can be moved.
A disc cannot be placed on top of a smaller disc.
Over the next exercises we gradually construct an mCRL2 specification of the
Towers of Hanoi puzzle. For this, we shall specify a Peg process to
represent a peg and we shall use a list to represent the contents of a peg.
The list data structure is predefined in mCRL2. All elements in a list must be
of the same type. This type is determined by the list’s type declaration, which
consists of the word List followed by the type of its elements between
parentheses. For example, a list l of natural numbers is declared by
l:List(Nat). Lists can be explicitly enumerated, so that [], [1],
and [2,3,5] are all valid list expressions, representing the empty list, the
list with single element 1 and the list with elements 2, 3 and 5, respectively.
Furthermore, the following operations on lists are provided:
cons
|>: insert an element at the front of a list, e.g.1 |> [2]gives[1,2];snoc
<|: insert an element at the back of a list, e.g.[2] <| 1gives[2,1];head: return the first element of a list, e.g.
head([1,2])gives1;tail: return a list without its first element, e.g.
tail([1,2,3])gives[2,3].
Note that the head and tail of an empty list are undefined, so that mCRL2 will
not further reduce the terms head([]) and tail([]).
The mCRL2 language supports more operations on lists, but they are not used in
this section. For the complete overview consult the
language reference.
We shall use lists to represent stacks of discs, such that the head of the list
corresponds with the top of the stack. A disc is represented by a positive
natural number, which is an element of the predefined data sort Pos.
Consider the following, incomplete data specification (available for download
as stack-holes.mcrl2:
sort Stack = List(Pos);
map empty: Stack -> Bool;
push: Pos # Stack -> Stack;
pop: Stack -> Stack;
top: Stack -> Pos;
var s: Stack;
x: Pos;
eqn empty(s) = ...; % return whether s is empty
push(x,s) = ...; % put x on top of s
pop(s) = ...; % remove top element from s
(!empty(s)) -> top(s) = ...; % return top element of s
This defines the Stack data sort as lists of positive numbers and declares
the functions (or maps) empty, push, pop and top as operations
on stacks. These functions have to be defined using equations, in which
variables can be used to represent any term of a certain type. For example, the
second equation defines push(x,s) for any positive number x and any
stack s, where variables x and s have been declared above the
eqn-block. Equations can also have guards which limit the set of terms to
which that equation applies. For example, the last equation defines top(s)
only for stacks s for which the guard !empty(s) holds, i.e. non-empty
stacks s.
Exercise
Complete the specification for the Stack data sort using the list
operations introduced above.
Solution
A possible solution to this exercise is the following (also available as
stack.mcrl2):
sort Stack = List(Pos);
map empty: Stack -> Bool;
push: Pos # Stack -> Stack;
pop: Stack -> Stack;
top: Stack -> Pos;
var s: Stack;
x: Pos;
eqn empty(s) = s == []; % return whether s is empty
push(x,s) = x |> s; % put x on top of s
pop(s) = tail(s); % remove top element from s
(!empty(s)) -> top(s) = head(s); % return top element of s
Observe that in this solution a number of choices have been made. Every
stack operation is directly mapped onto a predefined function on lists. As
pop is mapped to tail, pop is not defined on the empty stack.
An alternative would have been the following set of equations for pop:
var s: Stack;
x: Pos;
eqn pop([]) = [];
pop(x |> s) = s;
This definition does allow popping the empty stack. Observe how we used
pattern matching in the left hand side of the equation for the non-empty
stack.
Exercise
Your specification for the Towers of Hanoi puzzle has to be
parameterized by the number of discs N, such that changing the
value of N requires a change in one place of your specification only.
For this, introduce the following maps:
N: Pos, which holds the value ofN;build_stack: Pos # Pos -> Stack, which creates a stack of discs.
Define equations for the function build_stack such that
build_stack(x,y) returns the stack [x , x+1, ..., y] for any positive
numbers x and y. For example, build_stack(1,4) should return
[1,2,3,4]. For now, define N to be equal to 3.
Solution
This can be achieved using the following mCRL2 code:
map N: Pos;
build_stack: Pos # Pos -> Stack;
var x, y: Pos;
eqn N = 3;
(x == y) -> build_stack(x, y) = [x];
(x < y) -> build_stack(x, y) = x |> build_stack(x+1, y);
The stack specification, extended with N and build_stack is available
as stack2.mcrl2.
You can verify that the behaviour of the Stack data type, and the functions
defined on it, is as expected by opening the file in mcrl2xi. As
mcrl2xi expects a specification that includes a process as input
it is required to add the line
init delta;
to your specification (specifying the initial process). Now pushing the
Parse and type check button will parse and typecheck the
specifications. Any errors that occur will be reported. If your specification
parses and typechecks correctly, you can test the rewrite rules in your
specification. Enter e.g. build_stack(1,4) in the
Rewrite Data expression field, and press Rewrite. If
all is well, the tool reports the following in the Output window:
[08:34:30.908 info] Result: "[1, 2, 3, 4]"
Exercise
Specify the Peg process in mCRL2. It should have two parameters:
id: Pos, the peg’s number;stack: Stack, the peg’s stack of discs.
What actions can a single peg perform? What data parameters must these actions
have? Declare the actions first and then define the Peg process in mCRL2.
Solution
A peg can receive a disc from another peg, and it can send a disc
to another peg. The actions have three parameters:
a disc, the disc that is being moved,
the peg that the disc is moved from, and
the peg that the disc is moved to.
This results in the following declaration:
act receive, send: Pos # Pos # Pos;
A possible specification of the Peg process is the following.
proc Peg(id:Pos, stack:Stack) =
sum d,p:Pos . (empty(stack) || top(stack) > d) ->
receive(d,p,id) . Peg(id,push(d,stack))
+
sum p:Pos . (!empty(stack)) ->
send(top(stack),id,p) . Peg(id,pop(stack));
Exercise
Specify the initial process. Use the allow and comm
operators to enforce communication between the Peg processes.
Solution
The complete specification is given below, where the following actions are used:
move(d,p,q): discdis moved from pegpto pegq;receive(d,p,q): pegqreceives discdfrom pegp;send(d,p,q): pegpsends discdto pegq.
A move action is the result of synchronizing a send and a receive
action.
% Towers of Hanoi
map N: Pos;
eqn N = 3;
sort Stack = List(Pos);
map empty: Stack -> Bool;
push: Pos # Stack -> Stack;
pop: Stack -> Stack;
top: Stack -> Pos;
var s: Stack;
x: Pos;
eqn empty(s) = s == [];
push(x,s) = x |> s;
pop(s) = tail(s);
(!empty(s)) -> top(s) = head(s);
map build_stack: Pos # Pos -> Stack;
var x,y: Pos;
eqn (x > y) -> build_stack(x,y) = [];
(x <= y) -> build_stack(x,y) = push(x,build_stack(x+1,y));
act send, receive, move: Pos # Pos # Pos;
proc Peg(id:Pos, stack:Stack) =
sum d,p:Pos . (empty(stack) || top(stack) > d) ->
receive(d,p,id) . Peg(id,push(d,stack))
+
sum p:Pos . (!empty(stack)) ->
send(top(stack),id,p) . Peg(id,pop(stack));
init allow({move},
comm({send|receive -> move},
Peg(1,build_stack(1,N)) || Peg(2,[]) || Peg(3,[])
));
When generating the state spaces for N = 1,..., 6, we find that the
number of states is precisely 3^N.
The state space for N=3 is depicted in Figure State space of the Hanoi puzzle for 3 discs.
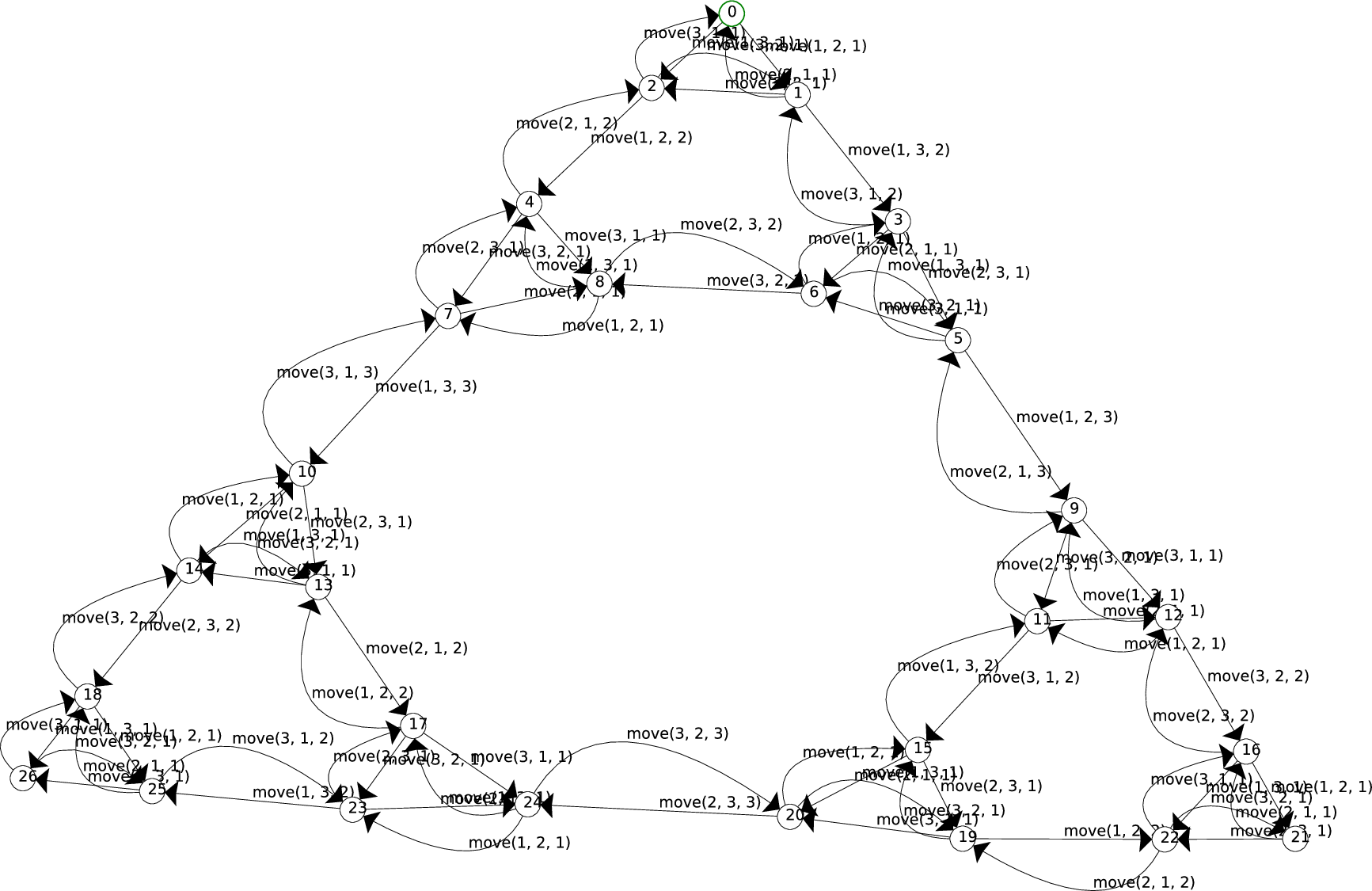
State space of the Hanoi puzzle for 3 discs
The above state space can be reproduced by the following commands:
$ mcrl22lps hanoi1.mcrl2 hanoi1.lps
$ lps2lts hanoi1.lps hanoi1.lts
$ ltsgraph hanoi1.lts
We use the tool lps2lts to see if there are any deadlocks by passing
the -D option:
$ lps2lts -D hanoi1.lps
No deadlocks are reported. This implies that this specification allows to
continue moving discs when the solution has already been obtained. We disallow
this by strengthening the guard for the send action in the Peg process
to:
!empty(stack) && !(#stack == N && id == 3)
This ensures that the system deadlocks when all discs are on peg 3. The
specification with this extension is available as hanoi2.mcrl2.
When checking for deadlocks of the new specification we find precisely
one, as expected. We save a trace to this deadlock in a file by adding the -t
option. The contents of the file can be printed using tracepp.
This is summarised by the following command execution:
$ mcrl22lps hanoi2.mcrl2 hanoi2.lps
$ lps2lts -D -t hanoi2.lps
deadlock-detect: deadlock found and saved to 'hanoi2.lps_dlk_0.trc' (state index: 26).
$ tracepp hanoi2.lps_dlk_0.trc
move(1, 1, 3)
move(2, 1, 2)
move(1, 3, 2)
move(3, 1, 3)
move(1, 2, 1)
move(2, 2, 3)
move(1, 1, 3)
This is a sequence of moves leading towards the solution. It consists of 7 moves. Because the default exploration strategy of lps2lts is breadth first search, we know that there is no shorter path to the solution. We now also prove that there is no shorter path to the solution using the µ-calculus. In fact, we shall prove two properties:
There is a sequence of \(2^N-1\) moves to a deadlock.
There is no shorter sequence of moves to a deadlock.
These properties are captured by the following µ-calculus formulae:
\((\mu X(n \colon \mathbb{N}) ~.~ (n = 2^N -1 \land [\top] \bot) \,\lor\, (n < 2^N-1 \land \langle \top \rangle X(n+1)))(0)\)
In ASCII syntax, this is represented as follows (available in
hanoi1.mcf% There is a path of 2^N - 1 steps to a deadlock (i.e. peg 3 has all % discs) mu X(n:Nat = 0) . (val(n == exp(2,N)-1) && [true]false) || (val(n < exp(2,N)-1) && <true> X(n+1))
\((\nu X(n \colon \mathbb{N}) ~.~ n \geq 2^N-1 \,\land\, ([\top] X(n+1) \lor \langle\top\rangle\top))(0)\)
In ASCII syntax, this is represented as follows (available in
hanoi2.mcf% There is no path shorter than 2^N - 1 steps to a deadlock nu X(n:Nat = 0) . val(n >= exp(2,N)-1) || ([true] X(n+1) && <true>true)
We check the formula on the specification by generating and solving PBESes as follows:
$ mcrl22lps hanoi2.mcrl2 | lps2pbes -f hanoi1.mcf | pbes2bool
true
$ mcrl22lps hanoi2.mcrl2 | lps2pbes -f hanoi2.mcf | pbes2bool
true
This yields true for both formulae, so both properties hold. Check these
properties for various values of N.
Optimal strategy
It is known that the shortest sequence of moves for solving the Hanoi puzzle
with N discs, is precisely the sequence that we obtain by repeatedly
alternating the following two moves until all discs are on peg 3:
Move the smallest disc one peg to the left if
Nis odd, and to the right ifNis even.Perform the move that does not involve the smallest disc.
For move 1 we consider peg 1 to be right of peg 3 and peg 3 to be left of peg 1. Observe that move 2 exists and is uniquely defined, except for the initial and final situations of the puzzle.
We now adapt our mCRL2 specification to model this optimal strategy only. In
other words, the state space of our model will only consist of the shortest
sequence of moves that leads to the solution. For this we first introduce a
function next that yields the next peg to which the smallest disc has to
move, according to move 1:
map next: Pos -> Pos;
var x:Pos;
eqn (N mod 2 == 0) -> next(x) = x mod 3 + 1;
(N mod 2 == 1) -> next(x) = (x-2) mod 3 + 1;
Our strategy for enforcing that only move 1 and move 2 occur alternatingly is to
add a fourth process to the model that allows precisely those moves only. This
process will take part in the synchronization of the send and receive
actions with an allowed action to produce a move action. We then rely on
the fact that all actions that participate in a synchronous communication have
to be present in order for that communication to succeed. This way, a move
can only occur if send, receive and allowed happen at the same
time, with the same parameter values.
The process that performs the allowed actions is actually modelled by two
processes: AllowSmall that allows move 1 and AllowOther that allows move
2. After performing an allowed action, every process then calls the other
process to ensure that move 1 and move 2 alternate indeed. Below are the action
declaration of allowed and the process definitions:
act allowed: Pos # Pos # Pos;
proc AllowSmall =
sum p:Pos . allowed(1,p,next(p)) . AllowOther;
AllowOther =
sum d,p,q:Pos . (d > 1) -> allowed(d,p,q) . AllowSmall;
Now, we enforce the aforementioned synchronization in the initial process
definition. Because move 1 comes first, we call AllowSmall in the parallel
composition.
init allow({move},
comm({send|receive|allowed -> move},
Peg(1,build_stack(1,N)) || Peg(2,[]) || Peg(3,[]) || AllowSmall
));
The full specification is available as hanoi3.mcrl2.
Generating the state space via mcrl22lps and lps2lts
yields 8 states and 7 transitions for N=3, obtained using the following
command sequence:
$ mcrl22lps hanoi3.mcrl2 hanoi3.lps
$ lps2lts -v hanoi3.lps hanoi3.lts
...
[12:38:30.547 verbose] done with state space generation (8 levels, 8 states and 7 transitions)
In general, the state space has \(2^N\) states and \(2^N-1\) transitions, as may be expected after our model-checking exercises on the complete model in the previous section. The action trace can be visualized by loading the state space into ltsgraph, or it can be simulated by loading the LPS into lpsxsim.